All crystals are divided into seven types of system, each of which has its own characteristic symmetry elements.
- Triclinic system - this type includes all crystals that do not have axes and planes of symmetry.
- Monoclinic system - this type includes all crystals that have 1 plane of symmetry or 1 double axis.
- Rhombic system - this type includes all crystals that have 3 mutually perpendicular double axes.
- Trigonal system - this type includes all crystals that have 1 triple axis.
- Hexagonal system - this type includes all crystals that have 1 hexagonal axis, that is, 1 axis of the sixth order.
- Tetragonal system - this type includes all crystals that have a 1/4 tetragonal axis, that is, a fourth-order axis.
- Cubic system - it is also called regular or isometric; this type includes all crystals that have 4 triple axes and 3/4 axes.
The triple axes are always parallel to the diagonals of the cube and slope at an angle of 70°32′ to one another. In some cases, the trigonal system of crystals may be part of the hexagonal system. All categories of syngony are divided into classes. There are 32 symmetry classes in total. Many classes are very rare in mineral formations.
There are types of system of didodecahedra class such as pentagon-dodecahedron
In each type of system, from the majority of known representatives, a degree of symmetry is found that is most suitable for this system. The holohedral class belongs to all types of system, but some types may also belong to several different classes.
Tetragonal system
This includes the holohedral class and the tetragon-bipyramidal class.
Holohedral class
A system of this class has a center of symmetry, one tetragonal axis, four double axes perpendicular to the tetragonal axis and five planes of symmetry located at right angles to all axes. It has a variety of special shapes in which a randomly located face is repeated in the form of 4 pairs of faces around the 4 axis and these faces are symmetrically displayed in the lower part of the crystal and form a ditetragonal bipyramid. This class includes zircon, vesuvianite and cassiterite.
Tetragon-bipyramidal class
A system of this class has a center of symmetry, one tetragonal axis and one plane located at right angles to the axis. It has simple forms of syngonies in the form of an octagonal tetragonal bipyramid in which there are no planes of symmetry passing through the tetragonal axis creating ditetragonal symmetry. It also has a special shape in the form of a pinacoid and tetragonal prisms. Scapolite belongs to this class.
Hexagonal system
This includes the holohedral and hexagon-bipyramidal class.
Holohedral class
This class is very similar to the holohedral class of the tetragonal system. A system of this class has a center of symmetry, seven planes of symmetry, one hexagonal axis, six double axes located at right angles to the sixth order axis. It has a general shape in the form of six pairs of faces that are symmetrically repeated and form a dihexagonal bipyramid. Beryl belongs to this class.
Hexagon-bipyramidal class
A system of this class has a center of symmetry, one axis of the sixth order and one plane located at right angles to the axis. Apatite belongs to this class.
singonia
(from the Greek “syn” - similar and “gonia” - angle) - in crystallography, a group of types of symmetry, which includes crystals that have similar symmetry elements and are characterized by certain geometric constants. There are seven systems in total (triclinic, monoclinic, rhombic, tetragonal, trigonal, hexagonal, cubic). Source:
Geological dictionary for schoolchildren, M, Nedra, 1985
Crystallographic system
, is a division of crystals based on the symmetry of their unit cell. Syngony is characterized by the relationships between axes a, b, c and angles a, b, g of the cell. There are 7 crystallographic systems: cubic (a = b = c, a = b = g = 90°), tetragonal (a = b ¹ c, a = b = g = 90°), hexagonal (a = b ¹ c, a = b = 90°, g = 120°), trigonal (a = b = c, a = b = g ¹ 90°), rhombic (a ¹ b ¹ c, a = b = g = 90°), monoclinic ( a ¹ b ¹ c, a = g = 90°, b ¹ 90°), triclinic (a ¹ b ¹ c, a ¹ b ¹ g ¹ 90°). Being the largest classification division in the symmetry of crystals, each system includes several point groups of symmetries and Bravais lattices.
In crystals, only 32 combinations of symmetry elements (32 types of symmetry) are possible; types of symmetry are combined into syngonies. Of the seven systems, the triclinic, monoclinic and orthorhombic systems are called the lowest because they do not have symmetry axes higher than the second order (L2). Trigonal, tetragonal and hexagonal systems are called average - they have one symmetry axis of higher order (L3, L4 or Li4), L6 or Li6. The cubic system has several higher order symmetry axes - L3, L4 or Li4 and is called the highest system. Syngonies are divided into 32 crystallographic classes (types of symmetry), including 230 space groups. These groups were first identified in 1890 by the Russian scientist E.S. Fedorov.
Sources:
- Great Soviet Encyclopedia.
- Popov G. M., Shafranovsky I. I. Crystallography, 5th ed., M., 1972.
- Smolyaninov N.A. Practical guide to mineralogy. M.: "Nedra", 1972.
32 types of symmetry are combined into syngonies.
There are seven syngonies in total. The name “syngony” comes from the Greek “sin” - “similar” and “gon” - “angle”. The syngony of a crystal is determined by the obligatory and similar symmetry elements for each system, as well as based on the presence or absence of single directions.
The unit direction (E) is the only direction in a crystalline polyhedron that is not repeated by any symmetry operations of a given group.
- The 7 syngonies are combined into three categories. The lowest category combines triclinic, monoclinic and orthorhombic systems. Crystals of these systems do not have symmetry axes higher than the second order.
- The middle category combines trigonal, tetragonal and hexagonal systems. Crystals of these systems have only one axis of symmetry of higher order (L3, L4, or L6), which coincides with a single unit direction.
- The highest category - cubic system - unites crystals that necessarily have 4L3. There are no single directions. All directions are symmetrically equal.
Names and formulas of 32 types of symmetry.
| Categories | Syngonies | Formula in Bravais symbolism |
| Lowest | Triclinic | L1; C |
| Monoclinic | R; L2; L2PC | |
| Rhombic | L22P; 3L2; 3L23PC | |
| Average | Trigonal | L3; L3C; L33P; L33L2; L33L23PC; |
| Tetragonal | L4; L4PC; L44P;L44L2;L44L25PC; Li4;Li42L22P | |
| Hexagonal | Li6=L3P; Li63L23P=L33L24P; L6; L6PC; L66P; L66L2; L66L27PC | |
| Higher | Cubic | 4L33L2;4L33L23PC;4L33L2(3Li4)6P;3L44L36L2; 3L44L36L29PC |
Source:
- Uspenskaya M.E., Posukhova T.V. Mineralogy with basics of crystallography and petrography
Trigonal system
It includes the holohedral, ditrigon-pyramidal, trigon-trapezohedral, ditrigon-bipyramidal and rhombohedral classes.
Holohedral class
A system of this class consists of a center of symmetry, one triple axis, three double axes that are perpendicular to the triple axis, and three planes located at right angles to the double axes. It has a general shape in the form of a scalenohedron which lacks a horizontal plane of symmetry. It also has a special shape in the form of a rhombohedron. This class includes hematite, corundum and calcite.
Ditrigon-pyramid class
The syngony of this class consists of one triple axis and three planes intersecting along the triple axis. They have a general shape in the form of a pyramid in which different ends of the crystal have different symmetries. They also have a special shape in the form of a trigonal or hexagonal prism with a cross section in the form of an equilateral triangle. Tourmaline belongs to this class.
Trigon-trapezohedral class
The system of this class consists of one triple axis, three double axes that are perpendicular to the triple axis. They have a general shape in the form of a right and left modification, which can be mirror-symmetrical or non-aligned. Quartz belongs to this class.
Ditrigon-bipyramidal class
The system of this class consists of one triple axis, three double axes located at right angles to the triple axis, one plane located perpendicular to the triple axis and three planes, each of which contains a triple axis and 1 double axis. This class includes one single mineral, benitoite.
Rhombohedral class
A system of this class consists of a center of symmetry and one triple axis. It has a general shape in the form of a rhombohedron. It also has a special shape in the form of a pinacoid and a hexagonal prism. This class includes willemite, phenacite and dioptase.
“...I believed
I algebra harmony. Then
Already dared, experienced in science,
Indulge in the bliss of a creative dream.”
A. S. Pushkin “Mozart and Salieri”
“Symmetry, no matter how broadly or narrowly we understand this word, is an idea
with the help of which man tried to explain and create order,
beauty and perfection"
Hermann Weil
I admit right away: there are practically no words of mine in this article. I took all the information from books and Wikipedia. And I compiled this short excursion into crystallography for myself, so that quickly forgotten pictures and examples would always be at hand. I would appreciate any additions or corrections.
So, we will talk about mineral crystals, the beauty and perfection of these creations of nature. Often people cannot believe that crystals are natural objects and not the creation of human hands. What is the secret of their beauty? And the first answer that comes to mind is their symmetry. Here a new concept already arises - symmetry, seemingly so simple and ordinary. But this is only at first glance. In fact, symmetry is a very complex and multifaceted phenomenon. It is studied by physicists, mathematicians, biologists, and even art historians. They have been studying it for more than a millennium, but the mysteries and questions are not decreasing. Let us wish our scientists new discoveries and Nobel Prizes, while we ourselves will dwell on geometric symmetry, which is necessary for the study of polyhedral crystals.
Geometric symmetry is the most well-known type of symmetry. A geometric object is said to be symmetrical if, after it has been transformed geometrically, it retains some of its original properties. For example, a circle rotated around its center will have the same shape and size as the original circle.
Crystals are solid bodies that have the shape of regular polyhedra acquired through natural growth. This form is a consequence of the ordered arrangement of atoms in the crystal, forming a three-dimensional periodic spatial arrangement - a crystal lattice.
In the lithograph by Maurits Cornelis Escher (Dutch artist, philosopher, mathematician and crystallographer) from the series ''Polyhedra'' there is a work entitled ''Order and Chaos''. In the center of the image is an ideal crystal of perfect shape, and around it are various deformed objects. And you don’t need any science to immediately subconsciously decide what is beautiful in this picture and what is not.
Symmetry is the primary diagnostic feature of minerals, so the basic concepts of crystallography must be understood and learned to use. In order to learn to recognize crystals and describe them correctly, you need to know the meaning of certain terms. It has long been noted that 90 percent of knowledge of any science is knowledge of terminology. According to the definition of symmetry given by mineralogist and crystallographer Evgraf Stepanovich Fedorov, “Symmetry is the property of geometric figures to repeat their parts, or, more precisely, their property in different positions to come into alignment with the original position.” Thus, a symmetrical object is one that can be combined with itself by certain transformations: rotations around axes of symmetry , center of symmetry , or reflections in planes of symmetry . So, first of all, symmetry elements are auxiliary geometric concepts that were introduced to describe the degree of symmetry of crystals (polyhedra). This is the center, axis and plane of symmetry.
a - plane of symmetry, b - axis of symmetry, c - center of symmetry
The center of symmetry (C) is an imaginary point inside the polyhedron. If you draw any straight line through this point, then on both sides of it this line will intersect identical (corresponding) points of the polyhedron. If there is a vertex on one side of C, then on the other side there is a vertex paired with it. The same applies to any points on faces and edges. You can check whether a crystal has a center of symmetry by placing the crystal on a horizontal surface. If all the faces and edges of a crystal are pairwise parallel and inversely equal, then there is a center of symmetry in such a crystal. If there is no center of symmetry, then there will be a vertex, edge or face at the top, but inclined or parallel, but not equal to the bottom.
The axis of symmetry (L) is an imaginary straight line, when rotated around which the polyhedron is aligned with its original position. The number of alignments during a complete rotation (360 degrees) around the axis of symmetry is the order of the axis of symmetry. Mineral crystals can have symmetry axes of only four orders: the second L2 (the crystal aligns with itself when rotated by 180 degrees), the third L3 (when rotated by 120 degrees), L4 (when rotated by 90 degrees) and L6 (when rotated by 60 degrees).
The ends of the symmetry axes in crystals can extend through the vertices, the centers of faces, or the midpoints of edges. When determining the axes of symmetry, it is by these elements that you need to take the crystal with two fingers and rotate it around this axis. In this case, the axis of symmetry should be positioned vertically, and the crystal should be kept at eye level.
If the crystal has three fourth-order axes, it is written as follows: 3L4, if there are four third-order axes - 4L3.
With a little practice, you can, for example, derive a formula that describes a cube and an octahedron: 3L44L36L29PC
The plane of symmetry (P) divides the polyhedron into two mirror-equal parts. A crystal can have one or more planes of symmetry, but not more than 9. To determine the plane of symmetry, we mentally dissect the crystal with a plane passing through its center. If to the left and right of this plane all parts of the crystal (faces, edges, vertices) are repeated as an object and its mirror image, then this is a plane of symmetry.
In many books they also use the concept “ Single direction ” - this is the only direction in a polyhedron that is not repeated in length. For example, in a pyramid or prism with a square base, this is their height.
Let's consider a few simple objects: a ruler, a pencil, a cube. They are all symmetrical, but their degree of symmetry is different. The most symmetrical is the cube, it is symmetrical on all sides. If you spin it and throw it in the air, you will see a spinning ball. Such crystals are called isometric. And no matter how you twist the pencil, it will not turn into a ball. Obviously, polyhedra differ in their degree of symmetry. To describe the degree of symmetry, all polyhedra were divided into 3 categories: lower, middle and higher, which in turn are divided into 7 crystallographic systems, which were called the word “ Syngony ”. In the lowest and middle categories there are 3 syngonies, in the highest - one. Let us now consider various crystals, grouping them according to the degree of symmetry, or according to belonging to one or another system, starting with the lowest, i.e. least of all symmetrical.
LOWER CATEGORY
Simple forms of crystals of the lowest category (triclinic, monoclinic and orthorhombic systems):
a - monohedron, b - pinacoid, c, d - planar and axial dihedrals, d - rhombic prism, f - rhombic tetrahedra right and left, g, h - rhombic pyramid and dipyramid
1. Triclinic system (parallelepiped)
In a triclinic system, of all the symmetry elements, only center C can be present. All directions in the crystal are single. All three axes have different lengths and intersect at sharp angles. This is the system with the lowest level of symmetry. The general shape is pinacoid; since each shape consists of a pair of parallel faces, at least three such shapes must exist in real crystals. Characteristic simple shapes: monohedron, pinacoid.
Monohedron Pinacoid Dihedron
Minerals that crystallize in the triclinic system: axinite, amblygonite, astrophyllite, turquoise, bytownite, wollastonite, kyanite, microcline, rhodonite, ulexite, plagioclase (albite - anorthite)
Kyanite crystal
2. Monoclinic system (prism with parallelogram)
In the monoclinic system, each symmetry element is present in the crystal in the singular. There are many individual directions. Three unequal axes, only two of them intersect at right angles. The common element of symmetry is the second-order axis L2 or plane P (at right angles to the axis) and the center of symmetry. Characteristic simple shapes: monohedron, pinacoid, dihedron, prism.
Minerals: azurite, monoclinic amphiboles (actinolite, arfvedsonite, glaucophane, hornblende, tremolite), arsenopyrite, orpiment, vivianite, wolframite, heulandite, gypsum, datolite, diopside, clinozoisite, crocoite, kunzite, malachite, orthoclase, petalite, monoclinic pyroxenes ( diopside, hedenbergite, augite, jadeite, aegirine, spodumene), realgar, micas, stilbite, sphene, talc, euclase, epidote.
Augite Gypsum
Datolite Clinozoisite
Orthoclase Mica phlogopite*
Spodumene Stilbite
* At first glance, it seems that at the base of the phlogopite crystal there is a regular hexagon, and this crystal should be classified as a hexagonal system, but when measuring the edges it turns out that they are slightly unequal; such crystals are called pseudohexagonal.
Aegirine Epidote
3. Rhombic system (rectangular parallelepiped)
In the rhombic system there are no axes of symmetry higher than the second order. The common symmetry element is 3L2 or L2, 2P. Three mutually perpendicular unit directions. The crystals have a rhombus cross section. Characterized by three unequal axes perpendicular to each other. Elements of symmetry: 3 unequal mutually perpendicular axes of the second order, 3 planes (at right angles to the axes) and a center of symmetry. Characteristic simple shapes: monohedron, pinacoid, dihedron, prism, pyramid, dipyramid, tetrahedron.
Minerals: andalusite, antimonite, aragonite, barite, hemimorphite, danburite, ilvaite, cordierite, marcasite, natrolite, peridot, rhombic pyroxenes (hypersthene, enstatite), prehnite, sulfur, staurolite, strontianite, topaz, chrysoberyl, celestine, cerussite
Barite Topaz
Danburite
Sulfur
MIDDLE CATEGORY
Prisms, pyramids and dipyramids of the middle category and their sections. a - trigonal, b - ditrigonal, c - tetragonal, d - ditetragonal, e - hexagonal, f - dihexagonal
Simple forms of crystals of the middle category: a - rhombohedron, b - trigonal scalenohedron, c - ditrigonal scalenohedron
Trapezohedra. a, b - trigonal right and left, c, d - tetragonal right and left, e, f - hexagonal right and left
4. Trigonal system (prism with the base of a regular centered triangle)
In the trigonal system there is one unit direction coinciding with the L3 axis. Characteristic element of symmetry: L3. Four axes: three equal, located in the same plane, the fourth unequal and perpendicular to them.
Characteristic simple shapes: monohedron, pinacoid, prism, pyramid, dipyramid, trapezohedron, scalenohedron, rhombohedron.
Minerals: hematite, dioptase, dolomite, ilmenite, calcite, cinnabar, corundum, quartz, magnesite, rhodochrosite, corundum, siderite, smithsonite, tourmaline, phenacite, chabazite, eudialyte
Quartz is ideal and real
Calcite Corundum
Tourmaline and its cross section in the form of a convex triangle
5. Tetragonal system (rectangular parallelepiped with a square at the base)
In the tetragonal (square) system, the common symmetry element is L4. Typically, crystals of this system have a square cross section and one unit direction coinciding with L4. Three axes are mutually perpendicular, two of them are equal to each other.
Characteristic simple shapes: monohedron, pinacoid, prism, pyramid, dipyramid, tetrahedron, trapezohedron, scalenohedron.
Minerals: anatase, apophyllite, vesuvianite, wulfenite, cassiterite, rutile, scapolite, chalcopyrite, zircon, scheelite
Vesuvian Zircon
Rutile
6. Hexagonal system (prism with the base of a regular centered hexagon)
In the hexagonal system, the one-unit direction coincides with L6. The common symmetry element for crystals of the hexagonal system is the L6 axis. Four axes: three equal, located in the same plane and intersecting at an angle of 60 degrees, the fourth unequal and perpendicular to them.
Characteristic simple shapes: monohedron, pinacoid, prism, pyramid, dipyramid, trapezohedron
Minerals: apatite, vanadinite, beryl, cancrinite, molybdenite, nepheline, pyromorphite, pyrrhotite
Apatite Beryl
Vanadinite
HIGH CATEGORY
Top grade crystal shapes
7. Cubic system
The cubic system has the highest degree of symmetry. The common element is 4L3. There are no single directions, all directions are symmetrically equal. The crystals are evenly developed in all directions; the crystal can be fit into a ball.
Typical simple shapes: cube, octahedron, tetrahedron, dodecahedron, didodecahedron.
Minerals: diamond, analcime, galena, halite, garnets, cuprite, lapis lazuli, loparite, magnetite, pyrite, pyrochlore, sodalite, sphalerite, tetrahedrite, fluorite, chromite, spinel.
Diamond Garnet almandine
Cuprite Magnetite
Pyrite
Fluorite Spinel
Crystallography describes ideal crystals, but we are dealing with real ones, which are often very different from their ideal prototypes. Here, for example, is what crystals of andradite, a cubic mineral, might look like in reality.
In addition, crystals of one mineral can have different shapes (calcite, for example, has several hundred such shapes), but the angles between their corresponding faces are unchanged - this is the basic law of crystallography. Now there are very good resources in which crystals are presented in the form of three-dimensional polyhedra, and even with the ability to twist them as you want. For each mineral there are several characteristic types of crystals. Look, for example, at this Mindat page: https://www.mindat.org/min-859.html, and you will see how easy and interesting it has become to study crystallography.
In conclusion, a little more theory. We often come across the fact that experts designate the edges of a crystal with some numbers in brackets, for example: (101), (001), etc. These notations are called face indices , and there is nothing complicated about these indices. The only difficulty is that you have to write about these spatial objects using flat pictures, and working with a single crystal will help much more than looking at hundreds of pictures. So, let's imagine the Cartesian coordinate axes XYZ, mark on each axis a segment equal to one or a, as in the picture, and imagine a plane that intersects the X axis at point a and is parallel to the YZ plane. This will be the plane (100). If we think a little, we will understand that all planes parallel to it will also have the same index. The plane parallel to the XZ plane has the index (010), and the parallel XY plane has the index (001). If we imagine a plane that intersects the X and Y axes at points a, and is parallel to the Z axis, then such a plane will have the index (110), etc. If a face is parallel to an axis, then its index along this axis is zero. The intersection with the negative part of the axis is indicated by a minus - a dash above the corresponding index.
As you can see, nothing complicated. All that remains is to agree on how to place the crystal in an imaginary coordinate system, because the position of its faces relative to the imaginary coordinate system depends on how the crystal is located in space. The general rule is this: the longest axis is combined with the Z axis. These rules are given in more detail in the table.
Cubic crystal system
It includes the holohedral, didodecahedral and tetrahedral classes.
Holohedral class
A syngony of this class consists of a center of symmetry, three fourth-order axes, four triple axes, six double axes, three planes located at right angles to the fourth-order axes, and six planes located perpendicular to the double axes. In diamond, the system has a simple shape in the form of a forty octahedron. This class can also have a special shape in the form of a cube, rhombic dodecahedron, octahedron, refracted cube, icositetrahedron and refracted octahedron. This class includes diamonds, fluorite, garnet and spinel.
Didodecahedral class
A system of this class consists of a center of symmetry, three double axes, four triple axes and three planes located at right angles to the double axes. It has a special shape in the form of a pentagon-dodecahedron, the so-called pyrotohedron. Pyrite belongs to this class.
Properties of minerals. Hardness, density, syngony, brilliance.
In the description of stones you can see a description of such properties as hardness, density, syngony and brilliance. At first, for me these description properties were meaningless words that I didn’t pay attention to at all. I think many of you will be interested to know what all the listed properties of minerals are. Not only interesting, but also useful information for the proper use of the mineral.
Hardness.
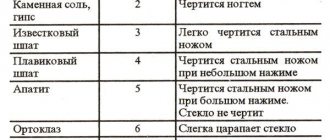
The hardness of stones is determined using the Mohs scale. For this purpose, a specially selected series of minerals is taken, which are arranged in order of increasing hardness: talc, gypsum, calcite, fluorspar, apatite, orthoclase, quartz, topaz, corundum, diamond. According to this scale, stones are divided into three groups:
- soft (1-2 units)
- medium (3-5 units)
— hard (6-7 units)
The hardness of the rock can be determined even more accurately using the PMT-3 device, the principle of which is to press a diamond pyramid into the sample
Hardness 1.2 - scratches with a fingernail.
Hardness 3.4, 5 - can be scratched with a knife.
Hardness 6 - scratchable with a file.
Hardness 7 - machinable.
Hardness 8.9 - scratches glass.
Hardness 10 - cuts glass.
Why is it necessary to know the hardness of purchased minerals or products made from them? For a basic storage rule. For example, the same balls of different minerals with different hardnesses must be stored separately from each other. A quartz ball can easily scratch the surface of a calcite ball. Or when we purchase two balls in order to “sort” them in the palm of our hands, we need to understand that high-hardness balls will be suitable for such purposes. Because balls of low hardness will get scratched very quickly and lose their original appearance.
Density.
Density is the mass of a substance per unit volume of a body. The density of natural stone directly depends on the composition of minerals and porosity.
In general, the higher the density of a mineral, the heavier it will be in weight.
Syngony.
Syngony is a group of types of symmetry that have one or more identical symmetry elements and have the same arrangement of crystallographic axes.
Crystallographic classes, or types of symmetry, are combined into larger groupings called systems or syngonies. There are seven such syngonies:
| Lowest | Triclinic | L1; C |
| Monoclinic | R; L2; L2PC | |
| Rhombic | L22P; 3L2; 3L23PC | |
| Average | Trigonal | L3; L3C; L33P; L33L2; L33L23PC; |
| Tetragonal | L4; L4PC; L44P; L44L2; L44L25PC; Li4; Li42L22P | |
| Hexagonal | Li6=L3P; Li63L23P=L33L24P; L6; L6PC; L66P; L66L2; L66L27PC | |
| Higher | Cubic | 4L33L2; 4L33L23PC; 4L33L2(3Li4)6P; 3L44L36L2; 3L44L36L29PC |
Highest category
Cubic system. The most symmetrical crystals crystallize in this system. In the cubic system there is more than one symmetry axes higher than the second order, i.e. L3 or L4. Cubic crystals must necessarily have four third-order axes (4L3) and, in addition, either three mutually perpendicular fourth-order axes (3L4) or three second-order axes (3L2). The maximum number of symmetry elements in the cubic system can be expressed by the formula 3L4 4L36L29PC. Crystals of the cubic system are found in the form of a cube octahedron, tetrahedron, rhombic dodecahedron, pentagon-dodecahedron, etc.
Average category.
Syngonies of the middle category. This group unites crystals that have only one symmetry axis of order higher than the second. The middle category includes hexagonal, tetragonal and trigonal systems. The hexagonal system is characterized by the presence of one sixth-order symmetry axis (L6). The maximum number of symmetry elements can be as follows" L56L27PC. Crystals of the hexagonal system form prisms, pyramids, dipyramids, etc.
Lowest category
In simple terms, the type of syngony is responsible for the shape of the crystal.
Shine.
The luster of minerals can be metallic (like most sulfides and native metals), semi-metallic (graphite, hematite) and non-metallic. Non-metallic luster is divided into:
- glass (fluorite, plagioclase; in general 70% of all known minerals),
- diamond (diamond, beryl),
- fatty (nepheline, sulfur),
- mother-of-pearl (opal, talc),
- silky (gypsum, hornblende),
- matte lack of shine (bauxite).
The brilliance of a mineral is primarily related to its refractive index. Metallic luster is characteristic of opaque minerals with a refractive index n > 3.0. Semi-metallic luster is observed in opaque minerals with n = 2.6-3.0. Diamond luster is found in minerals with n = 1.9-2.6. For minerals with a glassy luster, n = 1.3-1.9. Other types of shine appear due to the different structure of the surface of minerals. It should be noted that the same mineral can have different luster depending on the shape of the aggregates and on the cleavage plane along which it is cleaved.
I'll tell you in my simple language. When we try to describe something, we always resort to similar examples. The same goes for the shine of stones. If it is written that the shine is waxy, then just imagine the polished surface lightly coated with wax. Or, for example, glass glitter. Imagine how shiny the surface of the glass is.