Все кристаллы делятся на семь видов сингонии каждая из которых обладает своими характерными элементами симметрии.
- Триклинная сингония — к этому виду относятся все кристаллы которые не имеют осей и плоскостей симметрии.
- Моноклинная сингония — к этому виду относятся все кристаллы которые имеют 1 плоскость симметрии или 1 двойную ось.
- Ромбическая сингония — к этому виду относятся все кристаллы которые имеют 3 взаимно перпендикулярные двойные оси.
- Тригональная сингония — к этому виду относятся все кристаллы которые имеют 1 тройную ось.
- Гексагональная сингония — к этому виду относятся все кристаллы которые имеют 1 гексагональную ось то есть 1 ось шестого порядка.
- Тетрагональная сингония — к этому виду относятся все кристаллы которые имеют 1/4 тетрагональную ось то есть ось четвёртого порядка.
- Кубическая сингония — её еще называют правильная или изометрическая к этому виду относятся все кристаллы которые имеют 4 тройных оси и 3/4 оси.
Тройные оси всегда параллельны диагоналям куба и идут с уклоном под углом 70°32′ одной к другой. В некоторых случаях тригональная сингония кристаллов может являться частью гексагональной сингонии. Все категории сингонии делится на классы. Всего насчитывается 32 класса симметрии. Многие классы в минеральных образованиях встречаются очень редко.
Бывают виды сингонии дидодекаэдричесого класса такие как пентагон-додекаэдра
В каждом виде сингонии из большинства известных представителей обнаруживается степень симметрии которая максимально подходит для данной сингонии. Ко всем видам сингонии принадлежит голоэдрический класс но к некоторым видам могут принадлежать и несколько разных классов.
Тетрагональная сингония
К нему относится голоэдрический класс и тетрагон-бипирамидальный класс.
Голоэдрический класс
Сингония этого класса имеет центр симметрии, одну тетрагональную ось, четыре двойные оси перпендикулярные тетрагональной оси и пять плоскостей симметрии расположенных под прямым углом ко всем осям. Имеет разнообразные особые формы в которых произвольно расположенная грань повторяется в виде 4 пар граней вокруг 4 оси и эти грани симметрично отображаются в нижней части кристалла и образуют дитетрагональную бипирамиду. К этому классу относятся циркон, везувиан и касситерит.
Тетрагон-бипирамидальный класс
Сингония этого класса имеет центр симметрии, одну тетрагональную ось и одну плоскость расположенную под прямым углом к оси. Имеет простые формы сингоний в виде восьмигранной тетрагональной бипирамиды в которой нет плоскостей симметрии проходящих через тетрагональную ось создающих дитетрагональную симметрию. Также имеет особую форму в виде пинакоида и тетрагональных призм. К этому классу относится скаполит.
Гексагональная сингония
К нему относится голоэдрический и гексагон-бипирамидальный класс.
Голоэдрический класс
Этот класс очень схож с голоэдрическим классом тетрагональной сингонии. Сингония этого класса имеет центр симметрии, семь плоскостей симметрии, одну гексагональную ось, шесть двойных осей расположенных под прямым углом к оси шестого порядка. Имеет общую форму в виде шести пар граней которые симметрично повторяются и образуют дигексагональную бипирамиду. К этому классу относится берилл.
Гексагон-бипирамидальный класс
Сингония этого класса имеет центр симметрии, одну ось шестого порядка и одну плоскость расположенную под прямым углом к оси. К этому классу относится апатит.
Сингония
(от греч. «син» — сходно и «гония» — угол) — в кристаллографии группа видов симметрии, в которую входят кристаллы, имеющие сходные элементы симметрии и характеризующиеся определенными геометрическими константами. Всего имеется семь сингоний (триклинная, моноклинная, ромбическая, тетрагональная, тригональная, гексагональная, кубическая). Источник:
Геологический словарь для школьников, М, Недра, 1985
Сингония кристаллографическая
, — подразделение кристаллов по признаку симметрии их элементарной ячейки. Сингония характеризуется соотношениями между осями а, b, с и углами a, b, g ячейки. Существует 7 кристаллографических сингоний: кубическая (а = b = с, a = b = g = 90°), тетрагональная (а = b ¹ с, a = b = g = 90°), гексагональная (а = b ¹ с, a = b = 90°, g = 120°), тригональная (а = b = с, a = b = g ¹ 90°), ромбическая (а ¹ b ¹ с, a = b = g = 90°), моноклинная (а ¹ b ¹ с, a = g = 90°, b ¹ 90°), триклинная (a ¹ b ¹ c, a ¹ b ¹ g ¹ 90°). Являясь наиболее крупным классификационным подразделением в симметрии кристаллов, каждая сингония включает в себя несколько точечных групп симметрий и решёток Браве.
В кристаллах возможны только 32 сочетания элементов симметрии (32 вида симметрии), виды симметрии объединяются в сингонии . Из семи сингоний триклинная, моноклинная и ромбическая сингонии называются низшими, потому что они не имеют осей симметрии выше второго порядка (L2). Тригональная, тетрагональная и гексагональная сингонии называются средними, — они имеют одну ось симметрии высшего порядка (L3, L4 или Li4), L6 или Li6. Кубическая сингония имеет несколько осей симметрии высшего порядка — L3, L4 или Li4 и её называют высшей сингонией. Сингонии подразделяются на 32 кристаллографических класса (вида симметрии), включающих 230 пространственных групп. Эти группы впервые были выделены в 1890 русским ученым Е.С.Федоровым.
Источники:
- Большая советская энциклопедия.
- Попов Г. М., Шафрановский И. И. Кристаллография, 5 изд., М., 1972.
- Смольянинов Н.А. Практическое руководство по минералогии. М.: «Недра», 1972.
32 вида симметрии объединяются в сингонии. Всего различают семь сингоний.
Название «сингония» происходит от греческого «син» — «сходно» и «гон» — «угол». Сингонию кристалла определяют по обязательным и сходным для каждой сингонии элементам симметрии, а также, основываясь на наличии или отсутсвии единичных направлений.
Единичное направление (Е) — это единственное, неповторяющееся какими-либо операциями симметрии данной группы направление в кристаллическом многограннике.
- 7 сингоний объединены в три категории. Низшая категория объединяет триклинную ,моноклинную и ромбическую сингонии. Кристаллы этих сингоний не имеют осей симметрии выше второго порядка.
- Средняя категория объединяет тригональную, тетрагональную и гексагональную сингонии. Кристаллы этих сингоний имеют только одну ось симметрии высшего порядка (L3, L4, или L6), которая совпадает с единственным единичным направлением.
- Высшая категория — кубическая сингония — объединяет кристаллы, которые обязательно имеют 4L3. Единичных направлений нет. Все направления симметрично-равные.
Названия и формулы 32 видов симметрии.
| Категории | Сингонии | Формула в символике Браве |
| Низшая | Триклинная | L1; C |
| Моноклинная | Р; L2; L2PC | |
| Ромбическая | L22P; 3L2; 3L23PC | |
| Средняя | Тригональная | L3; L3C; L33P; L33L2; L33L23PC; |
| Тетрагональная | L4; L4PC; L44P;L44L2;L44L25PC; Li4;Li42L22P | |
| Гексагональная | Li6=L3P; Li63L23P=L33L24P; L6; L6PC; L66P; L66L2; L66L27PC | |
| Высшая | Кубическая | 4L33L2;4L33L23PC;4L33L2(3Li4)6P;3L44L36L2; 3L44L36L29PC |
Источник:
- Успенская М.Е., Посухова Т.В. Минералогия с основами кристаллографии и петрографии
Тригональная сингония
К нему относится голоэдрический, дитригон-пирамидальный, тригон-трапецоэдрический, дитригон-бипирамидальный и ромбоэдрический класс.
Голоэдрический класс
Сингония этого класса состоит из центра симметрии, одной тройной оси, трёх двойных осей которые перпендикулярны тройной оси и три плоскости расположенные под прямым углом к двойным осям. Имеет общую форму в виде скаленоэдра у которого отсутствует горизонтальная плоскость симметрии. Также имеет особую форму в виде ромбоэдры. К этому классу относятся гематит, корунд и кальцит.
Дитригон-пирамидальный класс
Сингония этого класса состоит из одной тройной оси и трёх плоскостей пересекающихся по тройной оси. Имеют общую форму в виде пирамиды у которой разные концы кристалла имеют разную симметрию. Также имеют особую форму в виде тригональной или гексагональной призмы у которой поперечное сечение в виде равностороннего треугольника. К этому классу относится турмалин.
Тригон-трапецоэдрический класс
Сингония этого класса состоит из одной тройной оси, трёх двойных осей которые перпендикулярны тройной оси. Имеют общую форму в виде правой и левой модификации которые бывают зеркально симметричными и несовмещающимися. К этому классу относится кварц.
Дитригон-бипирамидальный класс
Сингония этого класса состоит из одной тройной оси, трёх двойных осей расположенных под прямым углом к тройной оси, одной плоски расположенной перпендикулярно тройной оси и трёх плоскостей в каждой из которых содержится тройная ось и 1 двойная ось. К этому классу относится один единственный минерал бенитоит.
Ромбоэдрический класс
Сингония этого класса состоит из центра симметрии и одной тройной оси. Имеет общую форму в виде ромбоэдра. Также имеет особую форму в виде пинакоида и гексагональной призмы. К этому классу относятся виллемит, фенакит и диоптаз.
«…Поверил
Я алгеброй гармонию. Тогда
Уже дерзнул, в науке искушенный,
Предаться неге творческой мечты».
А. С. Пушкина «Моцарт и Сальери»
«Симметрия, как бы широко или узко мы не понимали это слово, есть идея,
с помощью которой человек пытался объяснить и создать порядок,
красоту и совершенство»
Герман Вейль
Признаюсь сразу: в этой статье практически нет моих слов. Я всю информацию взяла из книг и Википедии. И составила я этот краткий экскурс в кристаллографию скорей для себя, чтобы быстро забываемые картинки и примеры всегда были под рукой. Буду признательна за любые дополнения и исправления.
Итак, речь пойдет о кристаллах минералов, о красоте и совершенстве этих творений природы. Часто люди не могут поверить, что кристаллы – это природные объекты, а не создания рук человеческих. В чем же секрет их красоты? И первый ответ, который приходит на ум – в их симметричности. Тут уже возникает новое понятие – симметрия, казалось бы, такое простое и обыденное. Но это лишь на первый взгляд. На самом деле симметрия – очень сложное и многогранное явление. Ее изучают и физики, и математики, и биологи, и даже искусствоведы. Изучают не одно тысячелетие, а загадок и вопросов меньше не становится. Пожелаем же нашим ученым новых открытий и Нобелевских премий, а сами остановимся на симметрии геометрической, которая необходима для изучения кристаллов-многогранников.
Геометрическая симметрия — это наиболее известный тип симметрии. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг.
Кристаллы — твёрдые тела, имеющие приобретённую путём естественного роста форму правильных многогранников. Эта форма является следствием упорядоченного расположения в кристалле атомов, образующих трёхмерно-периодическую пространственную укладку — кристаллическую решётку.
В литографии Маурица Корнелиса Эшера (нидерландский художник, философ, математик и кристаллограф) из серии ‘‘Многогранники’’ есть работа под названием ‘‘Порядок и хаос’’. В центре изображения идеальный кристалл совершенной формы, а кругом различные деформированные предметы. И не нужно никакой науки чтобы сразу подсознательно решить, что на этой картине красиво, а что нет.
Симметрия – первостепенный диагностический признак минералов, поэтому основные понятия кристаллографии надо понять и научиться ими пользоваться. Для того, чтобы научиться распознавать кристаллы и правильно их описывать, необходимо знать значения некоторых терминов. Давно замечено, что 90 процентов знания любой науки – это знание терминологии. Согласно определению симметрии, данному минералогом и кристаллографом Евграфом Степановичем Федоровым, «Симметрия есть свойство геометрических фигур повторять свои части, или, выражаясь точнее, свойство их в различных положениях приходить в совмещение с первоначальным положением». Таким образом, симметричным является такой объект, который может быть совмещён сам с собой определёнными преобразованиями: поворотами вокруг осей симметрии, центра симметрии или отражениями в плоскостях симметрии. Итак, прежде всего, элементы симметрии – это вспомогательные геометрические понятия, которые введены для описания степени симметричности кристаллов (многогранников). Это центр, ось и плоскость симметрии.
а — плоскость симметрии, в — ось симметрии, с — центр симметрии
Центр симметрии(С) — это воображаемая точка внутри многогранника. Если через эту точку провести любую прямую линию, то по обе стороны от нее эта линия пересечет одинаковые (соответствующие) точки многогранника. Если по одну сторону от С находится вершина, то по другую сторону – парная ей вершина. То же относится к любым точкам на гранях и ребрах. Проверить есть ли в кристалле центр симметрии можно, положив кристалл на горизонтальную поверхность. Если все грани и ребра кристалла попарно параллельны и инверсионно равны, то центр симметрии в таком кристалле есть. Если центр симметрии отсутствует, то вверху окажется вершина, ребро или грань, но наклонная или параллельная, но не равная нижней.
Ось симметрии(L) – это воображаемая прямая, при вращении вокруг которой многогранник совмещается со своим первоначальным положением. Число совмещений при полном повороте (на 360 градусов) вокруг оси симметрии есть порядок оси симметрии. В кристаллах минералов могут быть оси симметрии только четырех порядков: второго L2(кристалл совмещается сам с собой при повороте на 180 градусов), третьего L3(при повороте на 120 градусов), L4(при повороте на 90 градусов) и L6(при повороте на 60 градусов).
Концы осей симметрии в кристаллах могут выходить через вершины, центры граней или середины ребер. При определении осей симметрии именно за эти элементы и нужно брать кристалл двумя пальцами и вращать его вокруг этой оси. При этом ось симметрии следует располагать вертикально, а кристалл держать на уровне глаз.
Если в кристалле имеется три оси четвертого порядка, это записывается так: 3L4, если четыре оси третьего порядка — 4L3.
Потренировавшись немного, можно, например, вывести формулу, которая описывает куб и октаэдр: 3L44L36L29РС
Плоскость симметрии (Р) делит многогранник на две зеркально-равные части. В кристалле может быть одна или несколько плоскостей симметрии, но не больше 9. Для определения плоскости симметрии кристалл мысленно рассекаем плоскостью, проходящей через его центр. Если слева и справа от этой плоскости все части кристалла (грани, ребра, вершины) будут повторяться как предмет и его зеркальное отражение, то это плоскость симметрии.
Во многих книгах пользуются еще понятием «Единичное направление» — это единственное, не повторяющееся по длине, направление в многограннике. Например, в пирамиде или призме с квадратным основанием это их высота.
Рассмотрим несколько простых предметов: линейку, карандаш, кубик. Все они симметричны, но степень симметрии у них разная. Самый симметричный – кубик, он симметричен со всех сторон. Если его закрутить и подкинуть в воздух, вы увидите вращающийся шар. Такие кристаллы называются изометричными. А карандаш, как ни закручивай, в шар не превратится. Очевидно, многогранники различаются по степени симметрии. Для описания степени симметрии все многогранники разбили на 3 категории: низшую, среднюю и высшую, которые в свою очередь подразделяются на 7 кристаллографических систем, которые назвали словом «Сингония». В низшей и средней категории по 3 сингонии, в высшей — одна.Рассмотрим теперь различные кристаллы, сгруппировав их по степени симметрии, или по принадлежности к той или иной сингонии, начиная с самой низшей, т.е. менее всего симметричной.
НИЗШАЯ КАТЕГОРИЯ
Простые формы кристаллов низшей категории (триклинной, моноклинной и ромбической сингоний):
а — моноэдр, б — пинакоид, в,г — диэдры плоскостной и осевой, д — ромбическая призма, е — ромбические тетраэдры правый и левый, ж,з — ромбические пирамида и дипирамида
1. Триклинная сингония (параллелепипед)
В триклинической сингонии из всех элементов симметрии может присутствовать только центр С. Все направления в кристалле единичные. Все три оси имеют разную длину и пересекаются под острыми углами. Это система с самым низким уровнем симметрии. Общая форма — пинакоид; поскольку каждая форма состоит из пары параллельных граней, в реальных кристаллах должно существовать не меньше трех таких форм. Характерные простые формы: моноэдр, пинакоид.
Моноэдр Пинакоид Диэдр
Минералы, кристаллизующиеся в триклинной сингонии: аксинит, амблигонит, астрофиллит, бирюза, битовнит, волластонит, кианит, микроклин, родонит, улексит, плагиоклазы (альбит — анортит)
Кристалл кианита
2. Моноклинная сингония (призма с параллелограммом)
В моноклинной сингонии каждый элемент симметрии присутствует в кристалле в единственном числе. Единичных направлений много. Три неравные оси, только две из них пересекаются под прямыми углами. Общим элементом симметрии является ось второго порядка L2 или плоскость Р (под прямым углом к оси) и центр симметрии. Характерные простые формы: моноэдр, пинакоид, диэдр, призма.
Минералы: азурит, амфиболы моноклинные (актинолит, арфведсонит, глаукофан, роговая обманка, тремолит), арсенопирит, аурипигмент, вивианит, вольфрамит, гейландит, гипс, датолит, диопсид, клиноцоизит, крокоит, кунцит, малахит, ортоклаз, петалит, пироксены моноклинные (диопсид, геденбергит, авгит, жадеит, эгирин, сподумен), реальгар, слюды, стильбит, сфен, тальк, эвклаз, эпидот.
Авгит Гипс
Датолит Клиноцоизит
Ортоклаз Слюда флогопит*
Сподумен Стильбит
* На первый взгляд кажется, что в основании кристалла флогопита лежит правильный шестиугольник, и этот кристалл следует отнести к гексагональной сингонии, но при измерении ребер оказывается, что они немного не равны, такие кристаллы называют псевдогексагональными.
Эгирин Эпидот
3. Ромбическая сингония (прямоугольный параллелепипед)
В ромбической сингонии отсутствуют оси симметрии выше второго порядка. Общим элементом симметрии является 3L2 или L2, 2Р. Три взаимно перпендикулярные единичные направления. Кристаллы в сечении имеют ромб. Характерны три неравные оси, перпендикулярные друг другу. Элементы симметрии: 3 неравные взаимно перпендикулярные оси второго порядка, 3 плоскости (под прямым углом к осям) и центр симметрии. Характерные простые формы: моноэдр, пинакоид, диэдр, призма, пирамида, дипирамида, тетраэдр.
Минералы: андалузит, антимонит, арагонит, барит, гемиморфит, данбурит, ильваит, кордиерит, марказит, натролит, перидот, пироксены ромбические (гиперстен, энстатит), пренит, сера, ставролит, стронцианит, топаз, хризоберилл, целестин, церуссит
Барит Топаз
Данбурит
Сера
СРЕДНЯЯ КАТЕГОРИЯ
Призмы, пирамиды и дипирамиды средней категории и их сечения. а- тригональная, б — дитригональная, в — тетрагональная, г — дитетрагональная, д — гексагональная, е — дигексогональная
Простые формы кристаллов средней категории: а — ромбоэдр, б — тригональный скаленоэдр, в — дитригональный скаленоэдр
Трапецоэдры. а,б — тригональный правый и левый, в,г — тетрагональный правый и левый, д,е — гексагональный правый и левый
4. Тригональная сингония (призма с основанием правильного центрированного треугольника)
В тригональной сингонии одно единичное направление, совпадающее с осью L3 . Характерный элемент симметрии: L3. Четыре оси: три равные, расположены в одной плоскости, четвертая неравная и перпендикулярная им.
Характерные простые формы: моноэдр, пинакоид, призма, пирамида, дипирамида, трапецоэдр, скаленоэдр, ромбоэдр.
Минералы: гематит, диоптаз, доломит, ильменит, кальцит, киноварь, корунд, кварц, магнезит, родохрозит, корунд, сидерит, смитсонит, турмалин, фенакит, шабазит, эвдиалит
Кварц идеальный и реальный
Кальцит Корунд
Турмалин и его поперечное сечение в виде выпуклого треугольника
5. Тетрагональная сингония (прямоугольный параллелепипед с квадратом в основании)
В тетрагональной (квадратной) сингонии общим элементом симметрии является L4. Обычно у кристаллов этой сингонии есть квадратное поперечное сечение и одно единичное направление, совпадающее с L4. Три оси взаимно перпендикулярны, из них две равны друг другу.
Характерные простые формы: моноэдр, пинакоид, призма, пирамида, дипирамида, тетраэдр, трапецоэдр, скаленоэдр.
Минералы: анатаз, апофиллит, везувиан, вульфенит, касситерит, рутил, скаполит, халькопирит, циркон, шеелит
Везувиан Циркон
Рутил
6. Гексагональная сингония (призма с основанием правильного центрированного шестиугольника)
В гексагональной сингонии одноединичное направление совпадает с L6. Общим элементом симметрии для кристаллов гексагональной сингонии является ось L6. Четыре оси: три равные, расположенные в одной плоскости и пересекающиеся под углом 60 градусов, четвертая неравная и перпендикулярная им.
Характерные простые формы: моноэдр, пинакоид, призма, пирамида, дипирамида, трапецоэдр
Минералы: апатит, ванадинит, берилл, канкринит, молибденит, нефелин, пироморфит, пирротин
Апатит Берилл
Ванадинит
ВЫСШАЯ КАТЕГОРИЯ
Формы кристаллов высшей категории
7. Кубическая сингония
Кубическая сингония отличается наибольшей степенью симметрии. Общим элементом является 4L3. Единичные направления отсутствуют, все направления симметрично равные. Кристаллы равномерно развиты по всем направлениям, кристалл можно вписать в шар.
Характерные простые формы: куб, октаэдр, тетраэдр, додекаэдр, дидодекаэдр.
Минералы: алмаз, анальцим, галенит, галит, гранаты, куприт, лазурит, лопарит, магнетит, пирит, пирохлор, содалит, сфалерит, тетраэдрит, флюорит, хромит, шпинель.
Алмаз Гранат альмандин
Куприт Магнетит
Пирит
Флюорит Шпинель
Кристаллография описывает идеальные кристаллы, а мы имеем дело с реальными, которые часто сильно отличаются от своих идеальных прототипов. Вот, например, как могут в реальности выглядеть кристаллы андрадита – минерала кубической сингонии.
Кроме того, кристаллы одного минерала могут иметь разную форму (у кальцита, например, таких форм несколько сотен), но углы между их соответствующими гранями неизменны – это основной закон кристаллографии. Сейчас появились очень хорошие ресурсы, в которых кристаллы представлены в виде объемных многогранников, да еще и с возможностью крутить их как захочется. Для каждого минерала представлено по нескольку характерных типов кристаллов. Посмотрите, например, на эту страницу Миндата: https://www.mindat.org/min-859.html , и вы убедитесь как теперь легко и интересно стало изучать кристаллографию.
В заключении еще совсем немного теории. Нам часто приходится сталкиваться с тем, что специалисты обозначают грани кристалла какими-то цифрами в скобках, например: (101), (001) и т.д. Эти обозначения называются индексами граней, и в этих индексах нет ничего сложного. Сложность заключается лишь в том, что писать про эти пространственные объекты приходится, используя плоские картинки, и работа с одним-единственным кристаллом поможет гораздо больше, чем рассматривание сотен картинок. Итак, представим себе декартовы оси координат XYZ, отметим на каждой оси отрезок, равный единице или а, как на картинке, и представим себе плоскость, которая пересекает ось X в точке а, и параллельна плоскости YZ. Это и будет плоскость (100). Если немного подумать, то мы поймем, что и все параллельные ей плоскости тоже будут иметь такой же индекс. Плоскость, параллельная плоскости XZ, имеет индекс (010), а параллельная XY– индекс (001). Если же представить себе плоскость, которая пересекает оси X и Y в точках а, и параллельна оси Z, то такая плоскость будет иметь индекс (110) и т.д. Если грань параллельна оси, то ее индекс по этой оси равен нулю. Пересечение с отрицательной частью оси обозначается минусом – черточкой над соответствующим индексом.
Как видим, ничего сложного. Осталось только договориться как размещать кристалл в воображаемой системе координат, ведь от того, как расположен кристалл в пространстве, зависит и положение его граней относительно воображаемой системы координат. Общее правило такое: самую длинную ось совмещают с осью Z. Более подробно эти правила приведены в таблице.
Кубическая сингония кристаллов
К ней относится голоэдрический, дидодекаэдрический и тетраэдрический класс.
Голоэдрический класс
Сингония этого класса состоит из центра симметрии, трёх осей четвёртого порядка, четырёх тройных осей, шести двойных осей, трёх плоскостей расположенных к осям четвёртого порядка под прямым углом и шести плоскостей расположенных перпендикулярно двойным осям. У алмаза сингония имеет простую форму в виде сорока восьмигранника. Также этот класс может иметь особую форму в виде куба, ромбододекаэдра, октаэдра, преломленного куба, икоситетраэдра и преломленного октаэдра. К этому классу относятся алмазы, флюорит, гранат и шпинель.
Дидодекаэдрический класс
Сингония этого класса состоит из центра симметрии, трёх двойных осей, четырёх тройных осей и трёх плоскостей расположенных под прямым углом к двойным осям. Имеет особую форму в виде пентагон-додекаэдра так называемый пиротоэдр. К этому классу относится пирит.
Свойства минералов. Твердость, плотность, сингония, блеск.
В описании камней можно увидеть описание таких свойств как твердость, плотность, сингония и блеск. Первое время для меня эти свойства описания были бессмысленными словами, на которые совершенно не обращала внимание. Думаю, многим из Вас будет интересно узнать, что из себя представляют все перечисленные свойства минералов. Не только интересной, но и полезной информацией для правильной эксплуатации минерала.
Твердость.
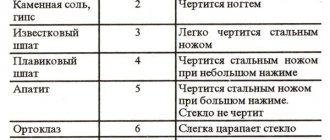
Твердость камней определяют по шкале Мооса. Для этого берётся специально отобранный ряд минералов, которые расположены в порядке нарастания твёрдости: тальк, гипс, кальцит, плавиковый шпат, апатит, ортоклаз, кварц, топаз, корунд, алмаз. По этой шкале камни делятся на три группы:
— мягкие (1-2ед.)
— средние (3-5ед.)
— твёрдые (6-7ед.)
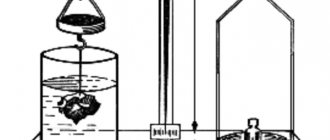
Ещё точнее твёрдость породы можно узнать с помощью прибора ПМТ-3, принцип работы которого заключается во вдавливании алмазной пирамиды в образец
Твердость 1,2- царапается ногтем.
Твердость 3,4, 5- царапается ножом.
Твердость 6- царапается напильником.
Твердость 7- поддается обработке.
Твердость 8,9- царапает стекло.
Твердость 10- режет стекло.
Для чего необходимо знать твердость приобретаемых минералов или изделий из них? Для элементарного правила хранения. Например, те же шарики из разных минералов необходимо с разной твердостью хранить отдельно друг от друга. Шарик из кварца легко может поцарапать поверхность шарика из кальцита. Или когда мы приобретаем два шарика для того чтобы из «перебирать» в ладони, необходимо понимать что для таких целей пригодны будут шарики высокой твердости. Т.к. шарики низкой твердости очень быстро поцарапаются и потеряют свой первоначальный внешний вид.
Плотность.
Плотность – масса вещества в единице объёма тела. Плотность природного камня напрямую зависит от состава минералов и пористости.
В общем, чем больше плотность минерала, тем он будет тяжелее по своему весу.
Сингония.
Сингонией называется группа видов симметрии, обладающих одним или несколькими одинаковыми элементами симметрии и имеющих одинаковое расположение кристаллографических осей.
Кристаллографические классы, или виды симметрии, объединяются в более крупные группировки, называемые системами или сингониями. Таких сингоний семь:
| Низшая | Триклинная | L1; C |
| Моноклинная | Р; L2; L2PC | |
| Ромбическая | L22P; 3L2; 3L23PC | |
| Средняя | Тригональная | L3; L3C; L33P; L33L2; L33L23PC; |
| Тетрагональная | L4; L4PC; L44P; L44L2; L44L25PC; Li4; Li42L22P | |
| Гексагональная | Li6=L3P; Li63L23P=L33L24P; L6; L6PC; L66P; L66L2; L66L27PC | |
| Высшая | Кубическая | 4L33L2; 4L33L23PC; 4L33L2(3Li4)6P; 3L44L36L2; 3L44L36L29PC |
Высшая категория
Кубическая сингония. В этой сингонии кристаллизуются наиболее симметричные кристаллы. В кубической сингонии присутствует более одной оси симметрии выше второго порядка, т. е. L3 или L4 . Кристаллы кубической сингонии обязательно должны иметь четыре оси третьего порядка (4L3) и, кроме того, либо три взаимно перпендикулярные оси четвертого порядка (3L4), либо три оси второго порядка (3L2). Максимальное количество элементов симметрии в кубической сингонии может быть выражено формулой 3L4 4L36L29PC. Кристаллы кубической сингонии встречаются в виде куба октаэдра, тетраэдра, ромбододекаэдра, пентагон-додекаэ дра и др.
Средняя категория.
Сингонии средней категории. Эта группа объединяет кристаллы, обладающие только одной осью симметрии порядка выше второго. К средней категории относятся гексагональная, тетрагональная и тригональная сингонии. Гексагональная сингония характеризуется наличием одной оси симметрии шестого порядка (L6). Максимальное количество элементов симметрии может быть следующим» L56L27PC. Кристаллы гексагональной сингонии образуют приз мы, пирамиды, дипирамиды и др.
Низшая категория
Если выражаться простым языком, тип сингонии отвечает за форму кристалла.
Блеск.
Блеск у минералов бывает металлический (как у большинства сульфидов и самородных металлов), полуметаллический (графит, гематит) и неметаллический. Неметаллический блеск подразделяется на:
- стеклянный (флюорит, плагиоклаз; в целом 70% всех известных минералов),
- алмазный (алмаз, берилл),
- жирный (нефелин, сера),
- перламутровый (опал, тальк),
- шелковистый (гипс, роговая обманка),
- матовый отсутствие блеска (боксит).
Блеск минерала связан прежде всего с его показателем преломления. Металлический блеск характерен для непрозрачных минералов, имеющих показатель преломления n > 3,0. Полуметаллический блеск отмечается у непрозрачных минералов с n = 2,6-3,0. Алмазный блеск встречается у минералов с n = 1,9-2,6. У минералов со стеклянным блеском n = 1,3-1,9. Прочие разновидности блеска проявляются в силу разной структуры поверхности минералов. Необходимо отметить, что один и тот же минерал может иметь разный блеск в зависимости от формы агрегатов и от того, по какой плоскости спайности он сколот.
Скажу своим простым языком. Когда мы пытаемся что-то описать, то всегда прибегаем к аналогичным примерам. Тоже самое и с блеском камней. Если написано, что блеск восковой, то достаточно себе представить отпалированную поверхность слегка покрытую воском. Или например блес стеклянный. Представьте как блестит поверхность стекла.